Nature's Numbers
by Bill Lauritzen
"By relieving the brain of all unnecessary work, a good notation system sets it free to concentrate on more advanced problems, and in effect increases the mental power of the race."
- A. N. Whitehead, author, An Introduction to Mathematics
"The discovery of a good counting system, which enables people to count better and more easily than their forebears did, means a great advance in civilization. Such discoveries are very rare."
- G. Flegg, author, Numbers Through the Ages
Preface
This book was prepared especially for the Columbus Day Lecture which I gave on October 10, 1994. It is a combination of two sources. First, a paper I wrote in 1992 called "Beyond the Hindu-Arabic Numeration System", and second, the overhead transparencies which I prepared for the lecture. In this second edition I have added additional, explanatory information to the figures as well as an afterward. I have reduced the importance of the round-hand model. Also, some corrections were made regarding my statements about Korzybski, about semantic response, as well as general corrections reflecting my most current thinking.
A larger book is planned, as well as a text for schools, but in the meanwhile it is hoped that this book will serve as an introduction to the subject.
I have left out information in order to be as clear as possible. Also, I have tried to err on the side of simplicity rather than complexity. I wish to communicate not obfuscate.
The name "nature's numbers" is interchangeable with the name "gravity-generated numbers." In the paper, I generally refer to them by the term "gravity-generated numbers."
A few words about the theorems mentioned. In a future book, I may offer more formal proofs. However, all of them can be proved experimentally. Use string, pennies (for circles), ping pong balls (for spheres), and straws.
The fact that there are only five regular polyhedron (also known as Plato's solids) is the climax of Euclid's Elements. The Pythagorean Theorem was, of course, known in the time of Pythagoras (6th century BC).
The rest of the theorems are not mentioned in Euclid, and so are not taught in schools today (1994 AD). This is unfortunate, as they are so easily demonstrated and on our spherical globe are more important than Euclid's primarily rectilinear geometry. We have to come forward nineteen centuries to Galileo to find mention of what I call the Maximum Area Theorem. Galileo proves this theorem in the Greek fashion in his Dialog Concerning Two New Sciences (1638).
Other theorems are derived from ideas I got from Fuller's works. I credit myself with formally codifying these ideas into theorems, thus giving them some of the recognition that they deserve.
Why these ideas are not generally recognized and taught is a good question. Perhaps, as suggested by Fuller, there has been a political-religious conspiracy to suppress knowledge of the round earth. Perhaps other books by Euclid, supposedly lost, contain this information.
The earth is round. Intellectually know it. Yet there persists a strong sense that the land is flat. That it extends infinitely. That there are three parallel planes: Heaven, Earth, and Hell. In a flat world, radiation from a nuclear bomb can blow away into infinity. In a round world, it may blow away, only to come around from the other side. So there are important consequences to having the correct model in our subconscious as well as our conscious.
There are many important new ideas in this book. Some of these are: circular place-value, the new numerical symbols, gravity-generated parallelogram multiplication, the triangular addition and multiplication table, the round-hand, and deriving geometry and numeration from gravity.
Another important I idea I have begun to investigate is how a number system affects the consciousness, the neurons, of the users. I suggest that a decimal, "base-ten" number system causes its users to be more violent and less sociable than a dozenal, "base-twelve" system. I believe a new field, which might be called sociomathematics, may eventually fully demonstrate this.
Some have asked me why I have bothered to develop a new number system. I answer why does anyone try to improve anything? If history is to be believed then numeral systems, like languages, evolve. I have little doubt that ten thousand years hence Hindu-Arabic numeration will have joined Babylonian, Roman, and Greek numeration on the scrap heap. In one sense, number systems are like mountains. Over one lifetime, mountains can seem relatively immovable, except for occasional earthquakes. Yet over the centuries they rise and fall. No, despite what we may think, numerals are not static.
In the year 1001 AD Hindu-Arabic numerals were virtually unknown on the European continent. If I had lived at another time, I might never have done what I have. Even though in a dozenal system there are no centuries and no millennia, I am a product of my time.
The thing to do now is to give these ideas a wide dissemination so that humankind can advance to a new, more intelligent way of thinking.
History
Hindu-Arabic numerals (O,1,2,3,4,5,6,7,8,9) have conquered the world. They are widely considered to be the most perfect numerals. But is there anything better? Or do we have the highly unusual situation of having attained a height beyond which we can go no higher? If we look to the sciences, we see men such as Copernicus, Galileo, Kepler, Newton, and Einstein, not content with the dogma of their day, and reaching out for better ways. Perhaps we have become content with the familiar.
Less than five hundred years ago, about the time of Columbus, most of Europe still calculated using an abacus and Roman numerals. (Ifrah, p.115) Although Leonardo Fibonacci introduced Hindu-Arabic numerals in 1202 AD in his book, Liber Abaci (A Book on Counting), it was not until the 15th and 16th centuries that interest in the new computational method blossomed. It was then that the common man (the tradesman, the merchants, and the surveyors) began to use the Hindu-Arabic numerals.
Hindu-Arabic numerals have their roots in India sometime before 300 BC. It is believed they evolved into a genuine place-value system in the 6th century AD. (Flegg, p.106) Shortly thereafter, when Arabia controlled the Middle East and its easy access to Asia, the numerals followed the trade routes and infiltrated Arab society. Several centuries passed, and there was a Renaissance in Europe concurrent with the introduction of the numerals there. (Perhaps Columbus used them.) Finally, in the 20th century, they established themselves in Asia.
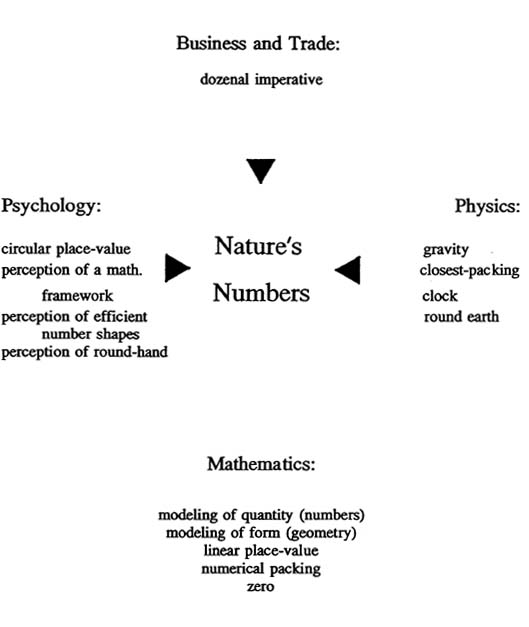
Our mathematics framework developed in ignorance of gravity and a round earth. I call this a pre-Newtonian (pre-gravitational) flat-earth framework.
I propose a more robust framework that utilizes gravity (or curved space-time in Einstein's model). Like Newton's theory of gravity, this new framework results in a vital shift in our perception of the surrounding universe.
I present a new number system corresponding to this framework, which I will compare to the Hindu-Arabic and other pre-gravitational mathematical number systems in order to show that my system is clearer, easier to learn, more efficient, has a firmer and more accurate connection to reality, and thus leads to greater awareness and mental acuity.
Finally, I show that the traditional, linear, "five-per-hand" concept, from which our own number system is derived, is really a primitive model unwittingly taught to us by our ancestors, and can be replaced by the circumscribed, "six-per-hand." This "circum-hand" conveniently aligns with a post-Newtonian, gravity-generated numerical framework, and can begin a major new step in mankind's evolving thought.
Terminology
It should be remembered that just because we use a base-ten number system during our discussion does not mean that we must unconsciously assume the superiority of base-ten. This is very important, and the reader should try to remember that in this manuscript, base-ten is a number system in question, rather than an unquestioned background assumption.
The Apollo pictures of Earth have developed a mass-conception by humanity of the spherical nature of Earth to the point where it is no longer necessary to use the words "up" and "down." They can be replaced by the words "in" and "out." In this same vein, I sometimes use the terms "group, grouping, module," or, my own innovations, "core, package, packing, or packed," when discussing number systems, rather than the more common "base." Since the word "base" implies a flat, rectangular plane, and thereby unconsciously affects our thinking, it is archaic and must go.
Simplicity
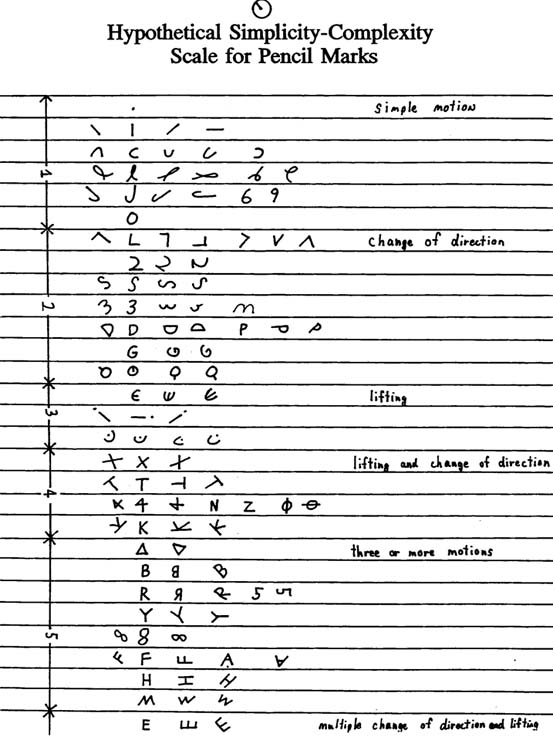
The simplest is probably a dot. However, a dot, by itself, can not indicate direction. Next in complexity, after a dot, probably is a line. After that might be a simple curve such as a "c". Although these could be placed in different orientations, the line indicates two directions at once, which is not sufficient for our purpose (except for perhaps a four-grouping system). The "c" is not precise enough. An arrow is too complicated a symbol because it requires lifting the writing instrument from the surface and then replacing it on the writing surface. Two dots also requires lifting the writing instrument and can not indicate direction. If we could take a simple line, and somehow put a "tail" on it, that would define a "head," and allow us to point it. Thereby we have direction.
Historical Numeration Systems
Hindu-Arabic, Chinese (stick), Babylonian, and Mayan numerical systems all are positional or place-value systems.
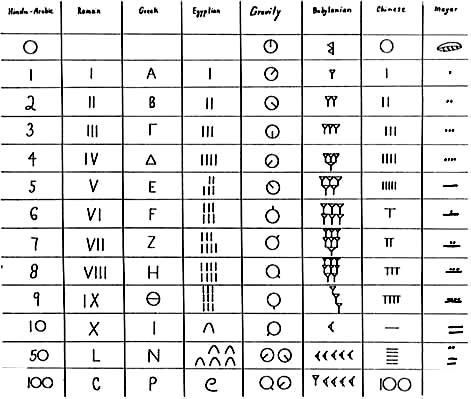
That is, the same symbol can be used over and over again but have a different meaning because of its location. For example, in the number, 333, the first 3 means three hundred, the next 3 means thirty, and the last 3 means three ones. Another example would be three vertical dots, in the Mayan system, representing 381. The highest dot represents 360, the next highest dot represents 20, and the lowest dot represents 1.
Mediterranean systems such as the Greek, Roman, and Egyptian hieroglyphic required the introduction of new symbols every time the quantity was increased by a significant amount. Thus the Greeks required their entire alphabet plus three additional letters for numerical representation. To write 358, the Greeks would write TNH, but 458 was YNH. In other words Y=400, but T=300. For this reason, the positional systems are usually considered more advanced. However, C. B. Boyer correctly notes that the Greek system is superior to the Babylonian for purposes of calculation, because of its economical use of symbols. (quoted by Flegg, p.90-96) More on this later.
Circumlinear Place-Value
Gravity-generated numerals take the positional system and extend it. The traditional positional systems use what I call "linear place-value." Hindu-Arabic, Chinese, and Babylonian are horizontal, while Mayan is vertical. Gravity-generated numerals use linear place-value as well as what I call "circular place-value."
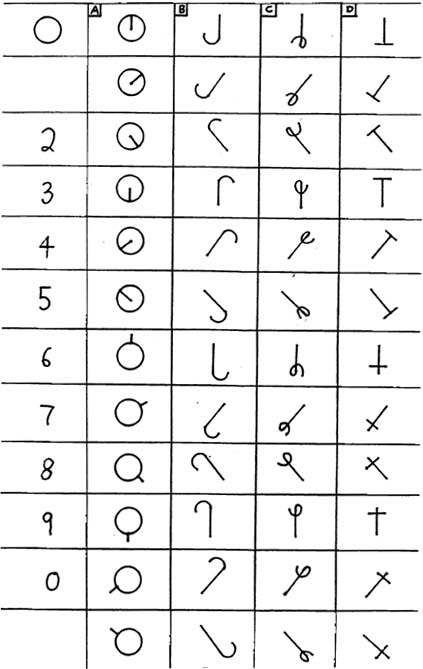
What is circular place-value? Our clocks use it. The Roman "I" on a clock can mean one hour, five minutes, or five seconds depending on which hand is being used.
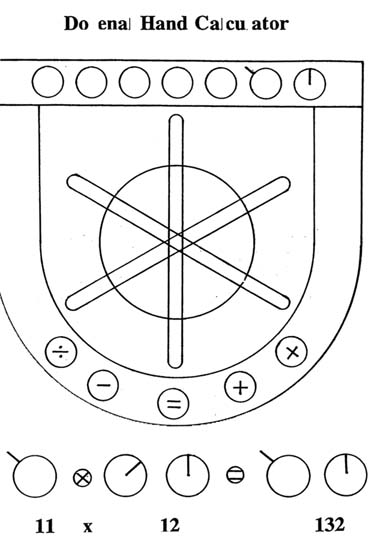
G-numerals extend the place-value concept. They follow the pattern of a mechanical clock with straight up being zero. Motion in a clockwise direction increases the number. Combining linear place-value and circular place-value produces what I call "Circumlinear place-value."
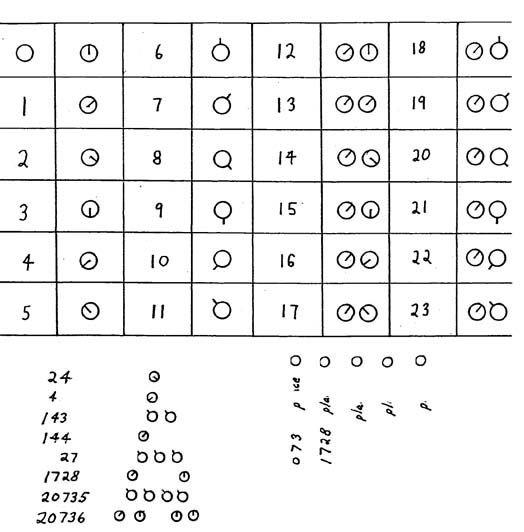
Circumlinear place-value is a great breakthrough in the field of numeration, and also in the field of symbolic communication. Although I use it here only for a 12-module system, it can be easily adapted for use with higher modules, and I expect it could be adapted for use with a computer and an alphabet.
However, despite its significance, it is by no means the most important aspect of this paper.
Gravity-Generated Symbols
There are four variations listed although there are others and the reader is encouraged to experiment to discover them. They all use twelve-packing rather than ten-packing. I explain why I chose twelve-packing later. The reader not interested in the specific details of these symbols and other ancient symbols can skip this section and the next.
Gravity-A numerals are more formal and perhaps more visually satisfying. Their circular shape is suggestive of the concept of gravity generation which also is explained later. They could easily be adapted to a computer printer or typewriter. Once we progress around the inside of the circle we move to the outside and repeat the pattern.
In gravity-B numerals we use a line with a tail or "hook." Gravity-C numerals are the same as gravity-B except we make a loop of the tail to indicate that we already have moved once around the circle already. Gravity-D was developed to demonstrate representation with straight lines rather than curves.
A "J" shape, as in gravity-B, is the simplest. Or a line with a simple loop at the end (like gravity-C). I believe that although a "J" looks simpler, the line with a loop is easier to make. This could be confirmed with tests. I think the reason for this is that the "J" requires careful attention at the lower part of the symbol in order to determine when to end it or to avoid crossing over the line. A line with a loop is a more carefree stroke because the line itself provides positive visual feedback as to when the loop has been finished. There is also a closure to the loop which is emotionally satisfying. An "L" shape, although not shown here, would also work.
I currently believe that the loop is the easiest to make. Scientific tests on groups of people (with the usual controls) should be done. I am not in a position to make these tests. However, I encourage others to do them, or to experiment with the various forms to see which they prefer.
The Hindu-Arabic system has nine symbols with which any number can be written, as the 6 and 9 are usually just upside down versions of the same symbol on a machine. The gravity-generation system can represent any number with the use of only two marks. For this reason I believe it would be easier to learn. (Also because of the widespread use of the mechanical clock.) It would be interesting to test this on young children.
Hindu-Arabic numerals vary in complexity. One might order them from simple to complex as follows: 1, 6, 7, 0, 2, 3, 9, 4, 5, 8. This order is based on the assumption that a straight line is simpler than a curve, which is simpler than a change of direction. "1" and "6" require a simple motion of the hand. "7", "2", "3", and "9" require two motions of the hand. "4", "5", and "8" require three motions of the hand. "0" requires only one motion, but because it is not a simple motion we put it with the numerals requiring two motions of the hand. Gravity-A would be somewhere in the two-motion category, while gravity-B and gravity-C would be in the one-motion category. For greater certainty, tests could be done.
For clarity, let's distinguish between a mark and a symbol. For example, the Roman symbol XII requires four separate marks.
The Chinese stick system which uses just one mark has been shown. (There were two other Chinese systems one of which is I believe much more popular.) From this stick they fashioned all their numerical symbols. Later they added zero. The Babylonians also used one mark: a wedge cut into clay. The Mayan system required three marks (a dot, a line, and their zero which resembled a shell). However, all three of these systems had the liability of having to repeat these marks several times in order to make the numerals 0-9. This required lifting the writing instrument from the paper (or bark, or clay, or papyrus) and then returning it. For example, the Babylonians had to make nine separate marks for 9, (later, they shortened it to three) and the Chinese and Mayans each had to make five. It is for this reason that C. B. Boyer considers the Greek system superior to the Babylonian for purposes of computation.
Like the Greek, the Hindu-Arabic requires few marks for 0-9. Hindu-Arabic has the advantage over the Greek in that all its symbols can be written without removing pen or pencil from paper. Of course, Hindu Arabic has place-value and Greek does not.
Gravity-A, B, and C have the advantage of numerical symbols that can be written with one mark and thus without removing pencil from paper. One easy way to write gravity-A is to put the pencil or pen down in the correct spot for that particular number, then make a circle, then make a mark going in or out.
Notice that in gravity-B it is possible to have a system that uses only one simple form, in twelve different orientations, to write any number from zero to (theoretically) infinity. There is the possibility that some of the orientations could be easily confused at a glance. However, I believe that familiarity would allow one to make the necessary discrimination quite easily. More research on this is needed.
Visual Acuity
I experimented on myself using larger numbers of divisions of the circle, from 6 to 24, but found that only with eight or less divisions was visual discrimination quick and accurate. Of course, if all the divisions of the circle are indicated with a mark, as on a clock, then divisions up to twelve are possible. Tests could be done to verify this.
Historical Uniqueness
It was not until after I had invented gravity-generated numerals that I began to investigate ancient number systems. I was sure that I would find something visually similar to a circular pattern, and was surprised when I did not. However, there are two reasons why circular forms probably have never existed. One, the mechanical clock has only been in widespread use for the past 300-500 years. (Ronan, p.37) People have not, until recently, been conditioned to think in terms of circular place-value. Two, when writing on clay, wood, or bark, as many ancient people did, it is much easier to chisel or cut a straight line than a circle.
Gravity-D requires no curves so this reason would not apply there. In fact, it was developed while searching for a numerical system that uses circumlinear place-value and no curves.
Shape
The shape of gravity-generated symbols reflects the shape that gravity imposes on the masses of the universe. The sun, moon, and planets are all approximately spherical.
The clock-like circular motion of gravity symbols also reflects the elliptical paths of the planets around the sun and the omnipresent rotation of objects in the universe.
Learning
Researchers such as Jean Piaget have studied extensively the learning of mathematics. Of course, post-gravitational mathematics, with its pictographic symbols, should facilitate concrete operational learning.
Hughes and others have discovered (1986) that pre-school children have some capacity to work with mathematical symbols for small numbers. I wonder at what age children could learn gravity symbols? One can easily imagine a movable clock-like hand that a child rotates in a circle to represent one apple, two apples, three apples, etc.
I predict that gravity symbols (or something similar) will alleviate some of the psychological problems traditionally associated with learning mathematics. I will discuss this in greater detail later.
Natural Intertransformations
The changes that occur in nature require exchange of particles, from microscopic to macroscopic. Human trade can be considered to be one type of macroscopic intertransformation which is of vital concern to us.
The science of economics has, at its core, this intertransformation. Commerce, business, marketing, etc. have at their core this intertransformation.
Thus, trade can be thought of as motion of particles (of some kind: food, money, etc.) from point A to point B, and the motion back from point B to point A of particles of a different kind. Upon examination, we see that these particles do not flow in a continuous stream of unitary size. In other words, we do not see quarks (lets consider this the most elementary particle) flowing one way and then quarks flowing the other way. What we see are groupings or packages of particles.
Thus, trade or intertransformation requires three things: 1) different kinds of particles, 2) ways of packaging these particles, 3) motion of these particles, and 4) ways of distributing these particles. Number 2 and 4 are vital problems of trade, economics, etc., and are of vital human concern.
Natural Grouping
As merchants pack goods, as elements pack atoms, so does humankind pack numbers. We do not see a continuous stream of IIIIIIIIIIII etc. The Romans packed numbers by 10, 50, 100, etc. with their symbols X, L, and C. The Babylonians packed them by 10s, 60s, etc. (Their grouping system is apparently where we derive our 60 minutes and 360 degrees in a circle.) Hindu-Arabic packs them by 10s, 100s, 1000s, etc. The Mayas used a modified twenty grouping (they used 360 rather than 400 for calendar coordination).
Although a larger grouping means a larger multiplication table to memorize, a 12 by 12 table is easy to memorize. In fact, most school children learn their elevens and twelves. (Instead of memorizing a 60 by 60 table the Babylonians wrote it down and referred to it when needed, much as we might use a calculator).
Despite efforts to squash it, twelve-packing seems to keep appearing in our culture. We have 12 inches to a foot, 12 to a multitude of products that come in a dozen, 144 or 12 times 12 to a gross, 12 ounces to a Roman pound, 12 hours to a Babylonian day, 12 old pence to a British shilling (although in 1971 the British decimalized their monetary system), and 12 times 2 hours in our own day.
Karl Menninger (1969, p.155) states that in Northern Europe, before the Christian influence, "hundred" meant ten 12s or 120. The term "great hundred" is still used to mean 120 fish.
Scholars of the past have suggested using twelve-packing as our standard packing. Simon Stevin suggested it in 1585 (Seely). In 1760, Georges Louis Leclerc, the Count of Buffon proposed it (Ifrah, p.35-36). In 1817, the U.S. Congress assigned John Quincy Adams to prepare a report on weights and measures (Ross, p. 73). Adams spent four years preparing a lengthy report, and became aware of a twelve-packing system. (Four years later he was elected president.)
The Dozenal Society of America, formerly the Duodecimal Society, is headquartered at Nassau Community College, Garden City, N.Y. It has collected some of the rather sparse historical literature regarding 12 systems. It also has explored and developed much of the mathematics of a dozenal system. (It frequently uses the symbols 0,1,2,3,4,5,6,7,8,9,*,# for 0 through 11, although they don't officially endorse any particular symbols.) It points out that the fractions 1/3 and 1/4 would not be never-ending decimals in a 12-grouping system. One-third, instead of being equal to .333333... would neatly resolve to .4. Two-thirds instead of being equal to .66666... would neatly resolve to .8. The reader who is interested in exploring the fascinating mathematics of a 12 system is encouraged to contact the society.
The main reason that has been given for twelve's advantage over ten, as a grouping system, is that twelve has 4 divisors (2,3,4,6,) and ten only has 2 (2,5). In other words, if you have twelve apples or twelve bundles of wheat, you can split it equally among 2, 3, 4, or 6 people. That is, you can half it, third it, quarter it, or sixth it. For businessmen, this provides a fluidity that is needed for efficient exchange of goods.
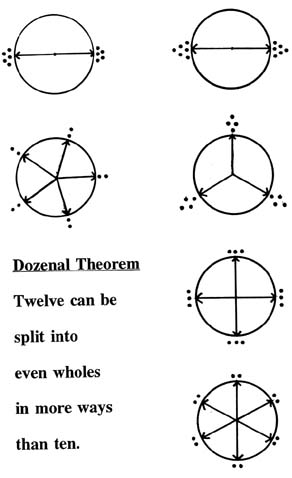
Look at the visual demonstration shown here. There are 2 groups at the top with their factors beneath them. (When I say factor here, I mean the numbers that divide evenly into another number, excepting the number itself and one.) If you had to choose between these two sides as methods of grouping, without actually counting how many are on the left and how many on the right, which would you choose? I think most people would choose the one on the right. For a twenty percent increase in numbers, from ten to twelve, you get a hundred percent increase in factors.
To use a real-life example, suppose a father brought home 12 apples, and told his children to divide them among themselves. If he has 2, 3, 4, or 6 children, then this is no problem. Now, suppose he brought home ten apples, and said the same thing. If he has 2 or 5 children, it is no problem. If he has 3, 4, or 6 children, then there could easily be arguments as to how to divide them. The children might decide to work out the fractions involved. But this activity takes time and effort, and meanwhile they are hungry.
Atoms, molecules, cells, mammals, cities, civilizations, and stars all exchange, borrow, and repay. Since nature always accomplishes its tasks using the minimum necessary effort (nature is lazy), we could expect nature to group by sixes and twelves rather than tens, much as many merchants already do. But does it?
Geometry and the Triangle
R. Buckminster Fuller has proposed what he calls "natures own coordinate system," which is not rectilinear (x,y) or cubical (x,y,z), but triangular or tetrahedral/octahedral. (1975, 1978, 1992) My proposal is for "nature's own numeration system."
When one looks at the frequent use of 3, 6, and 12 in the figures "Bucky" studied, one wonders why he didn't suggest changing to a twelve-core number system. He mentions (1975, p.729) that base 12 incorporates the triangle as well as the father-mother-child relationship, but then, in a rare, illogical moment, he analyzes a numeral in great detail from a base ten viewpoint. He apparently has an eccentric interest in base-10 numerology. However, all of his books are well-worth reading. For those who find his works difficult to understand, his recent book, Cosmography, and Amy Edmonson's book, A Fuller Explanation are helpful as starting places. In the next several paragraphs, let's examine some of his findings. Since this is a condensation of several large volumes of his works, it would be worthwhile to the reader to get some straws and string and build the models that I picture here. It will be difficult to understand what follows if you do not understand these models.

A triangle is the simplest polygon that will enclose space, as well as the only inherently stable structure in the universe. The photo shows how a triangle is stable, but a square is not. Polygons beyond the square (the pentagon, the hexagon, etc.) also are not stable. This is a very important fact that is almost completely overlooked in today's educational system. Many times I have drawn on the blackboard a square and a triangle and asked students which one will hold its shape better. It's not surprising when they select the square. Students seldom realize that the triangle, being the only stable polygon, is the starting point for all construction by nature, and I include man as part of nature.

The simplest polyhedron that will enclose space is the tetrahedron. The photo shows how a tetrahedron is stable, but a cube is not. This is because the tetrahedron is composed of triangles. The tetrahedron is composed of four sides. How many struts does it take to make one? Exactly six. Both of these numbers neatly divided into twelve.
The only other two regular, inherently stable structures besides the tetrahedron are the octahedron and the icosahedron. Both of these figures are stable because of triangulation.


The fact is that there is only one stable polygon (which encloses area), and only three regular stable polyhedra (which enclose space). All of these employ the triangle.
Thus, nature, if it is going to build anything, has to make use of the triangle. How can a number system that uses ten as its grouping system hope to accommodate nature? The answer, of course, is it can't.
Carbon Life
Organic life is the most intimate example of nature's order. Carbon, the organic atom from which life all stems, has an atomic number of 6, meaning it has 6 protons and 6 electrons. Frederick Kekule, the German chemist, had a famous dream in which he realized that carbon forms itself into hexagonal rings containing six atoms.
I recently participated in the "First International Interdisciplinary Fullerene Conference" to present a paper on the newly discovery spherical form of carbon, Carbon-60. Before this discovery, carbon was thought to exist in only two pure forms: graphite and diamond. Carbon-60, in it's most stable state, contains exactly 60 (12 x 5) carbon atoms, and, as stated in my paper, can be most effectively modeled using twelve triangulated pentagons, not the truncated icosahedron that is currently used. (See Photo 5) The hexagonal rings that Kekule dreamed of should also be shown triangulated.
Pre-life carbon, as it becomes orderly and grows, uses triangles, sixes, and twelves.
Gravity-Generation
How does gravity create twelve? We will use some of Fuller's work with closest-packed spheres. Although Fuller perhaps doesn't realize it, closest-packed spheres are a result of gravity-generation. In fact he uses the name "synergetics" to describe what might better be understood as "gravity-generated geometry." It's possible that he avoided the term I chose, "gravity-generation", because he didn't want to exclude Einstein's model of "curved space," but this is doubtful given his extensive use of the term gravity throughout his work.
I like the term "gravity-generation," because it communicates to a larger number of people than "curved space." Both Einstein's curved space as well as Newton's gravity result in the same closest-packing of spheres. If the mass of humanity had made the conceptual shift to space-time, I would use the word curved-space.
The choice of spheres is justified here as this shape is chosen by nature (for example, the earth) as combining the greatest internal space (volume) with the least surface area. Fuller (1975, p.418) shows how a balloon maintains it's shape by triangulations of the moving air molecules inside, and we can theorize that all spheres are microscopically triangulated.
A sphere (whether a ball, an orange, etc.) on a plane can be surrounded by exactly six spheres of the same size.

(See Fig. 7) If we then place another row of spheres around this row, it contains exactly twelve spheres. Additional layers also increase by adding six. This can be easily demonstrated with small discs such as pennies or with real spheres such as ping pong balls or clay balls.
The result shows how the grocer packs oranges together to get the most number of oranges in a crate. It has long been known that this is the best way to closely pack spheres. (Although it apparently has been proven by a mathematician only recently.) If the centers of the spheres are connected with straight lines, the hexagonal pattern of a bee hive is apparent.
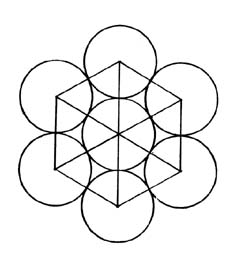
Bees use the hexagonal shape to provide the maximum space with the least amount of building material. Snowflakes also exhibit this hexagonal pattern. Again, these patterns, in which things fit together with the least waste of space, is most efficient and what makes nature most comfortable. Most school children would be hard-pressed to tell you this.
By the way, the word "grocer" comes from the word "gross." Literally, a grocer is one who packs by the gross. The derogatory meaning of "gross" undoubtedly came from people who couldn't stand the lack of correspondence between the way a grocer packed and the way Hindu-Arabic packed.
So in two dimensions we can see how gravity generates sixes and multiples of six. The old framework for mathematics would be ten balls in a row, and then rectangular extension of this. The hexagonal arrangement of the figure would be a good model for a core-6 system.
If one packs spheres in a three-dimensional layer around a central sphere, one will find exactly twelve in this layer. This is the shape created due to the natural force of gravity.

If additional spheres are added, the resulting figure maintains exactly twelve vertices. Gravity, one of the primary forces in the universe, always maintains this twelveness as it adds additional layers of spheres. This is again the way that the grocer packs oranges, and it can be easily demonstrated with clay balls.
We saw how a triangulated hexagon can be created by connecting the centers of closest-packed spheres. Every segment of this figure is exactly equal to every other segment. Only a hexagon has this ability: to radiate from its center with segments equal in length to its sides. In the above figure we see twelve spheres closest-packed around one.
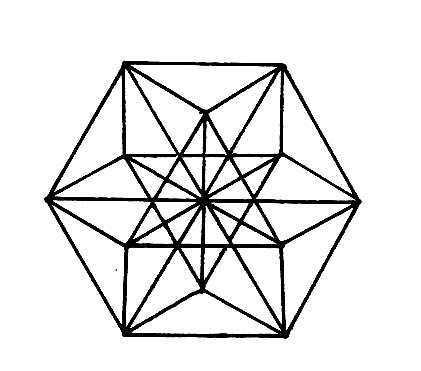
Here we have connected the centers of these spheres to create a figure that is the spacial counterpart to the hexagon we just left. In this case, there are twelve segments radiating from the center, and each of these segments is equal to the segments making up the sides of the figure. Only this figure has this spacial ability: to radiate from its center with segments equal in length to it outside segments. (Fuller calls this figure the Vector Equilibrium.)
The base-ten numeration system reflects a rectangular concept. Also, ignorance of closest-packing tends to make people conceive of "five in a row" or "ten in a row," and then ten more in the next row, and ten in the next row, etc. so that an unnatural rectilinear shape with a base is formed. Most of our houses are built with this shape (the necessary triangulation is usually hidden), but Fuller showed that by using a triangulated half-sphere, the geodesic dome, one can decrease the structural weight required to shelter a square foot of floor space from 50 to 0.78.
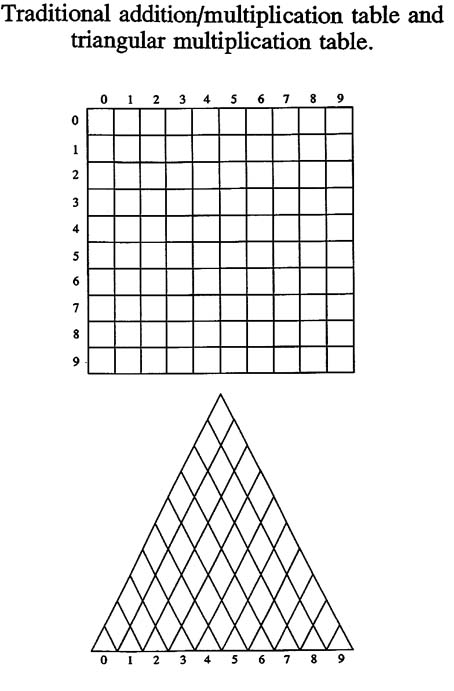
I have invented a triangular times-table to help counteract the early brainwashing of children by an exclusively square times-table. The new times-table is shown. It contains the same information, but in less area. Find two numbers along the bottom you wish to multiply, then make an equilateral triangle using the distance between the two numbers as one side of the triangle, and where they meet in the diamond is the answer. A similar table can be constructed for addition. I have used these tables effectively in the classroom. One is left incomplete as an exercise for the reader.
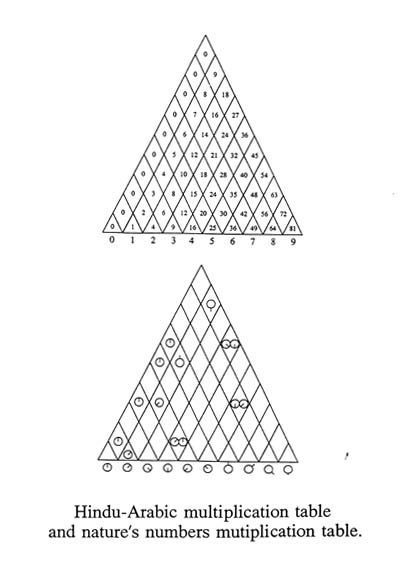
The misleading, square times-table is probably responsible for our term "perfect square" instead of the more correct "second power," since in the square table the second powers (4, 9, 16, 25, 36, etc.) all make squares rather than rectangles. Fuller effectively shows that the second power could just as easily be called "triangling" rather than "squaring." (Fig. 12) I noticed than one can get the ridiculous situation of calling the area of a circle, "pi times the radius squared." I require all my students to say "second power" unless the numbers specifically refer to square units of area.
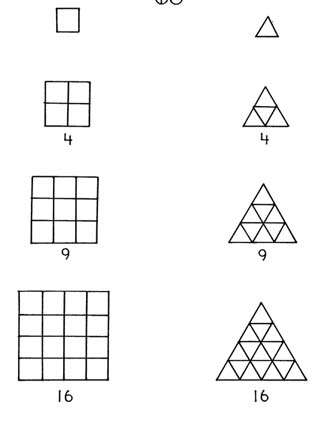
It appears that the second power, a number times itself, is somehow associated with area in general (at least with squares, triangles, and circles) rather than just with squares.
As a further example of how squares and rectangles have pervaded mathematics and geometry and made them unnecessarily complex, let's examine the word "plane." If you are like me, when you visualize a plane, you visualize it as a rectangular surface. That's the way it appears in all the geometry books. However, visualizing a triangular surface is just as valid as well as simpler. Imagine two points connected by a line segment. Now place a point next to the line just slightly above or below it. Connect that point to the two other points, and you have a triangle. In fact, upon examination I have found that the word "plane" is somewhat superfluous and can be replaced by the word "triangle." "Tri-plane" might be useful in breaking the rectangular monopoly. Three points, not in a line, always define a (tri)-plane as well as a triangle.
It's true that second powering is associated with area while third powering is associated with space. However, "two dimensions" means area, not a rectangle. The simplest two-dimensional figure is the triangle. "Three dimensions" means space, not a cube. The simplest three-dimensional figure is the tetrahedron.
I have invented a way to demonstrate multiplication using parallelogram arrays rather than the traditional rectangular arrays. (See figure.) This method would help to free the children from unnatural, rectilinear thinking and replace it with knowledge of closest-packing and triangular thinking.

Traditional rectangular multiplication is revealed to be a special case of parallelogram multiplication. So called "perfect squares" do not exist in nature. The simple and stable triangle can be used as an effective model for both addition and multiplication. All of chemistry and thus much of 1993 science is built on the idea of the simplest and smallest unit. The very word "atom" means "not divisible." Yet our entire mathematics of mensuration, stems from the complex and unstable square, instead of stemming from the most elemental and stable unit, the triangle. (Fuller, 1992) Area is measured in square feet. Volume is measured in cubic feet. Area could be measured in triangular feet, and volume could be measured in tetrahedral feet.
Rectangles do appear in the Vector Equilibrium shown earlier. However the figure could be made with just triangles. The rectangles appear as empty spaces between the triangles. It's possible that a triangle could represent order and the square disorder in the universe. Fortunately a 12-packed system embraces both numbers. So don't get the idea that I want to do away with all rectangles. I enjoy swimming in a rectangular pool. I just don't like rectangles as a framework for mathematics and geometry. They can be too easily pushed over.
Geometrical Arrays
We find that 10 things can be arranged (array-nged) evenly in only one way: a 2 x 5 array. Twelve things can be arranged three ways: 2 x 6, 3 x 4, or 2 x 3 x 2. This has important implications for merchants who are concerned with packaging, storing, and inventories.
We could say that twelve can be put together and taken apart evenly in more ways than ten. This is, I suspect due to the greater natural symmetry associated with twelve.
The Circum-Hand
There are a few examples in nature of the use of fives and tens. Both a sand dollar and a starfish have five radial extensions from the center. And ten balls can be stacked into a stable tetrahedral shape.
"And we have ten fingers!" you might be saying. One might wonder if this is some cruel joke by the Creator: to count by sixes or twelves and give man only five fingers.
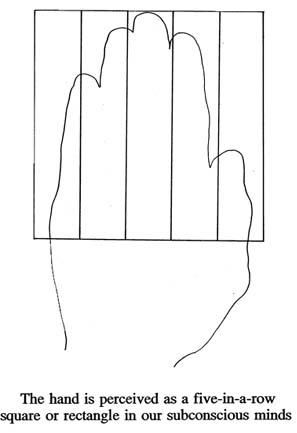
Of course, we really have only four fingers, with one thumb. This thumb is an opposable appendage, and that is very important because this opposition is the evolutionary advantage that enabled homo sapiens to grasp and use tools. This thumb is displaced from its opposing position and function, and made to lie, as an imposture, next to the longer and skinnier appendages in an attempt to form "five in a row". By saying "five fingers per hand" we are unconsciously idealizing a primitive, non-tool-using morphology. This leads back to where we came from.
However, even the four true fingers do not form uniform-length sticks or rods as is implied in our number system. On the contrary, when one examines them one is likely to be surprised at their varying lengths, for in our minds we have been conditioned by our current grouping system to think of them (all five) as being uniform in size and length. Their tips form the outline of a curve rather than a straight line. This hints at another possibility.
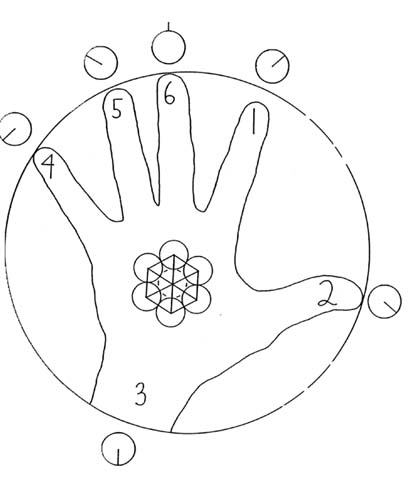
Study this figure. Notice that the human hand when maximally extended can make a fairly good approximation of the circle. If we now count the number of radial extensions we see six! Only now does the thumb seem to hold its own with the other four, and these four do not seem of such varying lengths as they did when we forced them to stand next to one another as if at a parade.
Is it possible that the human race has never learned to count in all these millennia? Like the schoolchild, who, when asked to count the number of people in the classroom, always forgets to count himself, have we forgotten to include the stem of our hand in our counting system?
Look at how humankind views nature. We commonly forget to include ourselves as part of it. Nature is in fact most often defined as anything that is not human or not built by humans.
Is it too much to imagine then, that we have forgotten to include ourselves, represented by the wrist, in our counting system?
Perhaps we still recall the time, at some impressionable age, probably much earlier than we suspect, when a grandparent, uncle, or parent, in an effort to advance us in knowledge beyond our peers, held up his or her hand and counted to five.
"Five fingers" was repeated so many times, and reinforced by our numerical system, that we learned to accept it without question.
Later, in school, we learned that there are twelve inches to a foot. This confused us, especially if we had not the advantage of working with an enlightened merchant. We may even have thought, "Why not ten inches?"
Then we were introduced to the metric system as being superior, and we accepted the centimeter, again without question. By the time we grew and became involved in the work-a-day world, where a practical knowledge of a dozen and a gross were useful, we had become so accustomed to ten that we may have wondered why dozens were even used. (It would be interesting to do a survey of businessmen to see if they use the dozen/gross and why.)
Let's call this new view of the human hand, with six radial extensions, the circum-hand (or hexa-hand or round-hand) and the old hand, the linear hand.
Can one count on one's fingers using the circum-hand. Certainly. With a little practice it's just as easy as counting by fives. One merely taps or flexes the wrist for six and its multiples. Perhaps an open palm with fingers together wound represent zero. Or perhaps the traditional circular shape for zero, made with the index finger and the thumb, would work. But old associations die hard, and the linear hand is one of the oldest. It would be interesting to teach some very young (un-brainwashed) children circum-hand association.
I introduced this concept once to a group of junior high students. Of course, by that age they are already thoroughly indoctrinated into a decimal system. Most of the students listened politely, but one stood up in the back of the room, pointed at me, and shouted, "you're crazy."
For much younger children, one could hold up an extended hand and ask them, "How many spokes?" Or one could ask them to imagine the sun at the palm of your hand and ask them, "How many rays are there?" If we can teach children to include themselves when they count the number of people in a room (which takes some effort), surely we can teach them to include their wrist as part of the anatomical representation of number.
I consider the development of the circum-hand, an alternative to "five-fingers-per-hand," to be an important step. However, it should be mentioned, that Ifrah states that counting on the three sections of the four fingers (using the thumb as a counter), which gives twelve, is a method of counting that is used in several countries. It may that this model is better than the six-per-hand model. (Although the spherical hand model reflects the spherical nature of things.)
Semantics, Psychology, and Numeration
The ten-core system may be responsible to some degree for human irrationality. Even the founder of General Semantics, Alfred Korzybski, was not aware of this. In Science and Sanity (p. 50), he states, mathematics ... the only language ever produced by man, which, in structure, is similar, or the most similar known, to the structure of the world and of our nervous system." He was right in seeing how words, language and language structure can blind us and affect our psycho-physiological system and human relations. That language, mathematics, which he held up to be most superior, was, in one sense, flawed, but this demonstrates his thesis: that our language and human structure unconsciously blind us.
Civilization and Numeration
A space-faring civilization would, I think, because of its more intimate association with the spherical gravity-generated nature of the articles of the universe, be more likely to use gravity-generated numerals. Thus, assuming there is intelligent life beyond earth, six-core, twelve-core, twenty-four-core, forty-eight-core, or sixty-core numerals may exist in some other part of the Galaxy.
If so, one wonders how that civilization might feel, when faced with a ten grouping system? Would they think that it was awkward, barbaric, complicated, insane, or frenzied? Will future generations, using a twelve-core system, look back on Hindu-Arabic numerals and feel the same way?
In fact, earth civilizations have attempted to use twelve, especially in measurement, and this would seem natural in light of what we have discussed. So why have we wandered off into the decimal, metric system?
In 1585, Simon Stevin, a Flemish mathematician, suggested a decimal arrangement of measures. In 1670, Gabriel Mouton made a similar proposal and submitted it to the French Academy of Science. Both proposals were forgotten.
After the American Revolution in 1776, Thomas Jefferson, Alexander Hamilton, and Robert Morris pushed for the adoption of a decimal monetary system which resulted in the Mint Act of 1792. This stated that "the money of account of the United States shall be expressed in dollars or units, dismes or tenths, cents or hundredths, and milles or thousandths". This was a break from the British halfpennies, pennies, threepence, sixpence, shillings, half crowns, pounds and guineas which had been in use. (A 1/2, 1, 3, 6, 12, 30, 240, 252 system that rather easily incorporated dozens.)
At the same time, Jefferson also proposed his own decimal system for weights and measures. However, Congress never acted upon it.
Across the ocean, back in France, another revolution was in progress that resulted in the guillotine for many and eventually in rule by Napoleon. Finally, the Paris Academy of Sciences, in 1791, recommended the decimal metric system to the French National Assembly, and several years later Napoleon mandated it in every country he conquered, even while he had trouble getting the commoners in his own country to use it.
In other words, not knowing the possibility of the circum-hand, or other models for counting, society has tried to bring measurement into line with the "five per hand" model. I believe that these were valid attempts at simplification, but not in the right direction. In all learning, there are mistakes and dead ends, and base-ten as well as metrics, are merely a wrong turn by humankind.
Twelve and dozens are used primarily because they allow for easy sharing. A numerical system that allows easier sharing has widespread implications that can only be faintly glimpsed at this point. Easier sharing means greater cooperation, easier distribution and more participation. On the contrary, a ten system or decimal system means less cooperation, more inefficient distribution, and less participation. Ten is less sociable than twelve.
Initial conditions can greatly affect later results. (This has recently been verified by research in chaos theory.) In fact, chaos theory has found that only slight changes in initial conditions quickly bring about widely diverging situations. Take two double pendulums and start them swinging from slightly different positions to verify this for yourself.
A civilization that starts on a ten-packed path will, I predict, evolve to a far different condition than one on a twelve-packed path. This difference may appear much sooner than we might expect.
A developing country (or any country) could decide to use natural twelve-packed numbers. The advantage this would give them over other countries would soon stimulate their economy, science and in general their culture, despite the fact that they might have limited natural resources.
I predict that a civilization organized according to natural, dozenal numeration will be a saner civilization, a better ordered civilization, and a faster growing civilization than one fixated on decimal numeration.
I predict that as yet undiscovered scientific principles, now obscured by our absolute acceptance and dependence on a base-ten numeration system, will become manifest if we shift into twelve-packed (or sixty-packed) numeration system.
I predict a renaissance on the order of that which accompanied the shift from Roman numerals to Hindu-Arabic. In other words, as Hindu-Arabic numerals accompanied the evolution of the sailing ship into the spaceship, so gravity-generated numerals (or something better) will accompany the evolution of the spaceship to the starship.
Natural Mensuration
Mensuration, like numbering, should be aligned as closely as possible with the way nature orders things. Would it not be simpler to keep twelve in a dozen, twelve inches, twelve and twenty-four hours, etc., and switch to a twelve-packed numeration system? Then we would have the advantages of a natural number system as well as the easy computation promised by the metric system.
The naturalness of the metric system can also be challenged ergonomically. I would hypothesize that an inch is near the optimum proportion to be of use by a human body, while the centimeter is too small. Which is why the inch developed in the first place.
There is a story that goes something like this: A civil engineer built a series of cement walks on a grassy college campus. However, they were not placed correctly and none of the students used them. The next time he was asked to build walkways, at another college, he waited until the students had used the grounds for some time, and then built the walkways where the grass had been worn down. Metric measurement ignores the worn grass that humanity has trampled down over the eons while trading with each other and attempting to measure the world, and tries to force us to walk where we don't naturally go.
Human Engineering
So human engineering is a part of all this. In fact, who is better qualified to develop new number systems, alphabets, symbols, or words than the human engineer? Traditionally, the human engineer has investigated the efficient design of human tools. What are language and mathematics if not human tools?
Binary Packing
Fortunately both ten and twelve incorporate the number two. However, some scientists believe that the best way to pack numbers is by 2s. This packing is currently in use by computing machines as it incorporates the "on/off" electrical switch. However, it is extremely cumbersome for use by humans. For example, 25 is written 11001.
Also, the binary system does not incorporate the unique stability and unitary simplicity of the triangle.
Six Hour Clock
Gravity numerals divide the circle into six parts whereas the clock divides it into twelve parts. This may cause some confusion. I suggest that these be brought into agreement. Since gravity numerals apparently require six divisions, then we must look at the possibility of changing the face of the clock.
Upon examination, there is no reason to require 12 rather than 6 divisions in the clock. The 24 hour rotation of the earth can be divided into night (midnight-6am), morning (6am-noon), afternoon (noon-6pm), evening (6pm-midnight). Thus, in the new system, 3 o'clock, could mean 3am, 9am, 3pm, or 9pm. Most people are sufficiently aware of the difference between these four parts of the rotation that this system would cause no problems. However, a letter could be added to the number when more certainty is needed. For example, 3:03a for morning, 3:03b for afternoon, and 3:03c for evening, and 3:03d for night.
Then, when children learn to tell time they would be learning a similar system to their numerical system.
New Theoretical Framework for Mathematics
Physicists accept gravity as one of the four primary forces of nature. Fuller suggests that it is one of the two primary forces: gravity spherically converging and radiation spherically diverging.
Why bring gravity into mathematics at all? As a matter of fact, mathematics is not necessarily formulated purely on abstract thought as some people might think. Pre-gravitational mathematics (such as Hindu-Arabic and the rest) is formulated on a definite physical law: two things made of the same substance can not occupy the same space at the same time. In other words, one apple plus one apple is two apples and no less. The two apples can not become one apple by occupying the same space. Also, we know that matter and energy cannot be created or destroy from nothing. So one apple and one apple can not equal three apples. Excuse me if I wish to be practical and give mathematics a solid core from which to grow.
Now one can ask, what other useful law holds true for two objects? They apparently have an attraction for each other due to gravity (or the curved shape of space). Thus we have gravity-generated numerals.
Mathematics and science have become increasingly hard to conceptualize. In fact, physics has become sufficiently divorced from conceptuality that we now have physicists making grand pronouncements about the birth and death of the universe and enjoying the role of priests. Perhaps this is part of the crisis that was needed before there can be searching and then acceptance of a new numerical framework. The "five-in-a-row" model was one of the first divergences of mathematics and science from the real world.
If we now go back and look at the figure of "12-around-1 sphere", I will summarize the new framework for mathematics.
Summary
The primitive Hindu-Arabic numeration system unconsciously and erroneously assumes a flat world and a linear row of "five fingers per hand." A primitive, linear place-value system limits the amount of information conveyed. It does not embrace the unique stability and simplicity of gravity.
My system, gravity-generated mathematics, conveys more information per symbol by use of circumlinear place-value, and uses grouping by 12 as: I) gravity always and only closest-packs spheres into a twelve-cornered configuration, II) the human hand with "five fingers in a row" is a primitive mythology taught to us by unwitting ancestors, when in reality there are four fingers, a thumb, and a wrist, which, when extended and circled neatly radiate six, III) nature always and only builds using the triangle, which is the only inherently stable polygon as well as the simplest area-enclosure.
These three facts are our primary observations, and we have the following derivative observations again from Figure 9: 1) from this symmetrical twelve-around-one packing we can connect the centers of the spheres by line segments, and have twelve radiating lines, 2) looked at from a (tri)planar viewpoint, we can derive a six around one packing, twelve-around-six packing, eighteen-around-twelve packing, etc., 3) from connecting the centers of these spheres we can derive the hexagon and the triangle, 4) in the hexagon we can see reflected the circum-hexa-hand, 5) from the circum-hexa-hand the human mind optimally remembers in the short term six, 6) twelve's geometrical symmetry, again in the 12-around-1 spheres, is responsible for the fact that twelve can be put together or taken apart in more ways than ten, which gives it greatly increased potential for exchange in nature's perpetual intertransformation, 7) twelve's ability to be split up evenly in more ways than ten allows for greater opportunity for equal sharing, which has far-reaching implications for commerce and social cooperation.
Thus, by using a tangible, omnipresent, force of nature on spheres so that they closely pack 12 around 1, and combining this with two hexagonal circum-hands as a corresponding anatomical reference and powerful visual image, I provide a conceptual, general, easily understood, and more robust framework than that which has existed for mathematics, and give dozenal numerical packing justification.
Conclusion
Obviously, this paper is intended to stimulate research by professional educators, psychologists, mathematicians, human engineers and others. It is also intended to inform and educate the intelligent layman and teacher, as they are the ones ultimately who make the decisions about the numerical system society uses, regardless of lofty pronouncements in scholarly journals.
Also, I hope to stimulate people to look for and question unconsciously held beliefs as did Copernicus, Newton, Einstein, and Fuller.
This model is not a perfect model. It might have been convenient if, as we added layers of spheres to the twelve-around-one, each layer increased in multiples of twelve. However, nature found it more convenient to do otherwise.
But, do not condemn this model for its lack of perfection. If Newton's theory of gravitation had been required to achieve perfection, his book, Mathematical Principles of Natural Philosophy, probably the most influential book in the history of science, would never have been published, and we would never have heard of gravity. He and others of his time were painfully aware that gravity required "action at a distance." (How does something here affect something over there? when there is apparently nothing between them.) Although nowadays we accept action across a distance, especially with radio and television, without really understanding it, at that time there were fewer examples of it. (The magnet would be one.) This action at a distance was (and still is) a glaring deficiency of the theory of gravity that most textbooks today skip over. However, his model was better than any other that existed at that time. Thus, the only valid criterion for gravity-mathematics, or any new model, is whether or not it is better than the old model.
Obviously, it's my belief that gravity-generated dozenal packing is better than decimal, "five-in-a-row" packing. Early education in "six-per-hand" or the "hexa-hand," or the twelve finger-segments per hand model, could put a great, new tool in humankind's grasp. A tool that only has been dreamed of by some practical mathematical visionaries of the past: a twelve-packed numeration system.
How long would this take to occur?
In 1299 AD, the city of Florence issued an ordinance prohibiting the use of Hindu-Arabic numerals because they were easier to falsify than Roman numerals. (Flegg, p.128) For example, a 0 can be easily changed to a 6 or a 9. That's probably why we still write out, in letters, the amounts on checks. Hindu-Arabic numerals, after they evolved into a true place-value system, took a good fourteen centuries to spread through the world.
People and cultures change their traditions slowly, and with good reason. If society changed course every time some Johnny-come-lately had a new idea, it would end up nowhere. New ideas must be thoroughly tested in the no-nonsense world of food production, engineering and commerce.
Thanks to people like Arthur C. Clarke (the first to conceive of the communications satellite) we have almost instant global communications. So perhaps a twelve-packed numeration system won't take as long to spread as Hindu-Arabic numerals.
The best thing for progress would be to have an enlightened leader who instructed his or her scientists and mathematicians to write new textbooks that incorporated decimal as well as twelve-packed numbers until enough people understood the new system. The other possibility is a grass-roots movement.
However, looking at recent historical events, the momentum is on the side of the metric system and base-ten. Here in the United States, base-ten is unconsciously accepted. Metric measurement is quickly reaching the same status. Until recently, I vigorously taught these two systems as though they were the last best systems. Civilization could, perverted by an erroneous number system and unable to accept a new one, deteriorate to a stone age. The Mayans, as far as we know, never did invent the wheel.
It will take some extremely brave souls to challenge decimal numeration and measurement, and a lot of very hard work to turn the tide. But the rewards will be worthwhile.
Mathematicians have known that twelve has more factors than ten. Merchants have known that twelve has more flexibility than ten. However, they have not been successful in overthrowing the Decimal King. In fact, these dozenal disciples have always been outside the castle walls, just annoying the Decimal Court with their "numerical factors" and their "dozens." Thanks to the "five-per-hand" model, they have fought a losing battle. However, despite heavy losses they have somehow kept the dozenal torch lit.
The fact is, the decimal fortress would not fall because the dozenalists had no firm model with which to attack. Now, with the development of the alternatives to "five-per-hand", and gravity-generated numeration, the castle walls can finally be scaled, and the corrupt Decimal Dynasty can come crumbling down.
You can count on it.
| DATE | Events in Numerical History |
|---|---|
| 30,000 B.C. | Marks like I, II, III. Notches on bones. |
| ? | Numerical bases first developed. |
| ? | Ancient merchants use dozen and gross. |
| 1900-1800BC | Babylonia uses place value, base-60 numeration system. |
| 200 BC | Primitive 1-9 symbols in use in India. |
| 300-400 BC | Mayans use place-value, base-20 numeration with zero |
| 600 AD | Place-value and zero used in Hindu System. Similar to our current system. |
| 800 AD | Northern Europeans use ten 12s as their "hundred." Survives as "great hundred." |
| 1202 AD | Fibonacci writes about Hindu-Arabic numerals. |
| 1400-1500 | Hindu Arabic numerals become widespread in Europe during their renaissance. |
| 1586 | Decimal fractions are popularized by Simon Stevin thus simplifying notation. He also proposes a base-twelve number system. |
| 1686 | Newton unifies motion on earth with the motion of the planets in one of humankind's greatest conceptual leaps: the law of gravity. |
| 1760 | Georges Louis Leclerc proposes adoption of a base-twelve system. |
| 1785 | The U.S. goes onto a decimal money system. |
| 1790-1840 | During the time period of the French Revolution, France invents and then uses metric measurement. |
| 1821 | John Quincy Adams presents a report on weights and measures to U.S. Congress and mentions a twelve-based number system. |
| 1944 | The Duodecimal Society of America forms, largely at the instigation of F. Emerson Andrews, stressing the greater factorability of twelve. Later, their name is changed to the Dozenal Society. |
| 1971 | The British switch to decimal money system. |
| 1930-1970 | R. Buckminster Fuller develops a natural, synergetic geometry as shown in the geodesic dome. |
| 1992 | Bill Lauritzen develops the gravitational-accumulation of spheres, circumlinear place-value, and simple circular twelve-packed symbols. |
Note: Some of these dates have been adapted from Ifrah. However, I am continuing to research in this area. Ancient dates are always approximate and archeological discoveries can radically change priorities and dates. It is possible that Chinese discoveries predate some of the discoveries mentioned here, but since the Babylonians wrote on clay tablets that are well preserved, we have much better records of Babylonian developments. Further investigation may show that ancient man had a far greater grasp of mathematics than we usually give him or her credit for.
Afterward
Note that some gravity generated spheres are equally distant from their center of gravity. (One could also say symmetrical shapes in which every sphere has an equal position in relation to every other sphere.) This equally symmetrical gravitational accumulation only occurs with the following numbers of spheres: 1, 2, 3, 4, 6, and 12. These correspond to a point, a line, a triangle, a tetrahedron, an octahedron, and an icosahedron.
This is counter-intuitive. One thinks that if one just keeps adding spheres that one can eventually get a regular, symmetrical shape. But flat areas and corners appear. Twelve is the limit. We can codify this into a theorem: Gravity Accumulates Spheres Into Six And Only Six Regular Shapes.
Let's discuss this from a wider perspective. Some physicists think (1995) that there existed before the Big Bang a completely symmetrical state. Total symmetry would be a featureless state where nothing could be distinguished from anything else. They think that after the Big Bang this total symmetry broke and resulted in the various degrees of degradation existing in our universe.
I believe that a possible useful model for of mathematics is: 1) total symmetry, 2) the universe, 3) gravity, 3) geometry, 4) mathematics. Each state derives from the previous.
We know that geometry means "measurement of the earth." We think that the earth formed as a result of gravitational impact of particles. Thus it should be obvious that geometry derives from gravity even without the study of gravitational packing of spheres.
In the book Fearful Symmetry, there is a picture of a drop of milk hitting a bowl of milk. Before the drop hits the surface of the bowl, that surface provides an extremely symmetrical (featureless) shape. When the drop hits there are exactly twenty-four nearly equal splashes formed which radiate outward and upward. We see nature and gravity breaking symmetry by using a multiple of twelve.
One can image an intermediate state of twelve.
It is becoming clear to me that the social aspects of a dozenal number system are quite large. Because a dozen can be shared equally in more ways than ten, I believe that ten has become associated, in our minds, due to times of hardship, with more stress than a dozen. Ten results in more a) physical stress, or more b) mental stress. I think the physical stress results because ten forces conflict as humans struggle for that extra piece or those extra pieces left over. Mental stress results if the human has to use fractions or infinite decimals to divvy up ten.
Repeat to yourself -- ten, ten, ten.
Repeat to yourself -- dozen, dozen, dozen.
I feel more relaxed after saying -- dozen. I think that perhaps in my "subconscious mind," I have learned than with a dozen there is less need to fear.
Since our mind works by association, perhaps using various social systems (numbers, measurement, money) that are derived from ten constantly keeps ourselves in a level of stress that is harmful and unnecessary.
It is my belief that by deriving from nature and gravity a new geometry and numeration, and by realizing that it is a more sociable geometry and numeration, we can ultimately make a more intelligent and cooperative civilization.
References
Boyer, C.B., "Fundamental Steps in the Development of
Numeration," Isis, Vol. 35, p.157-158. Boyer, C.B., A History of
Mathematics, Wiley, 1968.
Carey, S. Warren, Theories of the Earth and Universe, Stanford University Press, 1988 (p. 365 for opening quotation.)
Edmonson, Amy, A Fuller Explanation, Birkhauser, Boston, 1987.
Flegg, Graham, Numbers Through the Ages, Macmillan, 1989. (opening
quotation p. 17.)
Fuller, R. Buckminster, Synergetics, 1975, See also Synergetics
Vol.II, 1979, Cosmography, 1992, all published by Macmillian, N.Y.
Hogben, Lancelot, Mathematics for the Million, Norton, N.Y., 1960, p. 297 for abacus.
Hubbard, L. Ron, Basic Study Manual, Bridge Publications, 1992.
Hughes, Martin, Children and Number, Basil Blackwell, 1986.
Ifrah, Georges, From One to Zero, Viking Penguin, N.Y., 1985.
Josefsberg, Milt, Comedy Writing, Harper and Row, N.Y., 1987.
Korzybski, Alfred, Science and Sanity, 3rd ed., Business Press, Lancaster, Pa., 1948.
Lauritzen, W.G., "Buckminsterfullerene Triangulated," presented at
the "First International Interdisciplinary Fullerene Conference," Santa
Barbara, July, 1993.
Menninger, Karl, Number Words and Number Symbols, MIT Press, 1969.
Piaget, Jean, Child's Conception of Number, Routledge and Kegan Paul, London, 1965.
Resnitoff, H.L. and Wells, R.D., Mathematics and Civilization, Dover, N.Y., 1984.
Rogers, James T., The Story of Mathematics, Hodder and Stoughton, London, 1979.
Ronan, Colin, Lost Discoveries, McGraw-Hill, N.Y., 1973.
Seely, Howard F., Manual of the Dozenal System, The Dozenal Society of America, N.Y., 1960.
Stewart, Ian and Golubitsky, Martin, Fearful Symmetry, Penguin Books, N.Y., 1992.
Struik, Dirk J., A Concise History of Mathematics, Dover, N.Y., 1984.
ACKNOWLEDGEMENTS: Gene Zirkel of the Dozenal Society. Pat Millington. Jennifer Mooney. I'd like to especially thank my friend Peter Johnston.
For Further Information:
Buckminster Fuller Institute
2040 Alameda Padre Serra Suite 224
Santa Barbara, CA 93103
Dozenal Society of America
Math Depatment
Nassau Community College
Garden City, LI, New York 11530